|
Terraforming Model Equations. |
By Christopher P. McKay, NASA-Ames Research Center, c.1994; temporarily extended by Martyn J. Fogg, Probability Research Group, 1999.
Cover note
: This provisional essay covers the algorithm at the heart of the Terraforming Calculator V1.1 and has been extended from the notes for V1.0 by Fogg (modifications in blue text). When a new text has been prepared by McKay and his students, it will be posted as a replacement.1.0 Introduction.
To warm Mars above its present temperature or to maintain a N2/O2 atmosphere warm will require either lowering the surface albedo, increasing the energy deposition, or enhancing the greenhouse effect. To achieve any of these effects require production of the appropriate material on Mars. Various planetary engineering methods have been suggested to do this.
|
Warming Effect |
Planetary Engineering Method |
|
Lowering the planetary albedo |
Darken the surface with dust and/or plants |
|
Increasing energy deposition |
Supply more sunlight with orbiting mirrors |
|
Enhancing the greenhouse effect |
Increase the abundance of greenhouse gases |
One of the features of the surface energy balance is that the rate of warming due to any single effect diminishes with increasing amount. For example the amount of warming that is produced by the first added 100 hPa (mbar) of CO2 exceeds that warming resulting from the second 100 hPa of CO2.
This has led to the observation that the best way to warm Mars is to use several effects together (Fogg, 1992). Each is pushed to the practical limit and a synergistic effect results.
In order to combine the effect of changes in the albedo, energy deposition, and greenhouse gases we need to have a physically based model of surface energy balance. We express the surface energy balance as
![]() (Eq.1)
(Eq.1)
where s is the Stefan-Boltzman constant, Ts is the globally averaged surface temperature, a is the globally averaged surface albedo, Sm is the solar constant at Mars orbit, Fg is the flux incident on the surface due to the greenhouse effect of the atmosphere.
In principle one can solve Equation 1 for the surface temperature but the difficulty arises in computing the greenhouse flux, Fg. We wish to have an efficient method for computing Fg for a combination of possible greenhouse agents, including CO2, H2O, CH4, NH3 and CFCs. To approach this problem we note that the flux from each greenhouse gas is approximately independent of the flux from other gases. Thus we let
![]() (Eq.2)
(Eq.2)
This allows us to combine expressions for the greenhouse effect of individual gases to obtain an estimate of the total resultant effect.
In obtaining expressions for the flux from each individual greenhouse agent we utilize the solution of the surface and atmospheric temperature profile for an atmosphere that absorbs uniformly at all wavelengths. In this case the greenhouse heating is given by
![]() (Eq.3)
(Eq.3)
which in Equation 1 reduces to
![]() (Eq.4)
(Eq.4)
where t is the equivalent grey opacity of the greenhouse gas. It is clear then that
![]() (Eq.5)
(Eq.5)
where Tb is the effective temperature of the planet given by
![]() (Eq.6)
(Eq.6)
and the t terms refer to the equivalent grey opacity of each individual greenhouse agent, S with no subscript refers to the energy deposited on Mars normalized to the present solar flux, Sm. (Artificially increasing the energy deposition on Mars involves increasing the S term, increasing the greenhouse effect involves increasing the t terms, and lowering the albedo involves reducing the a term.)
2.0 Greenhouse Gas Equations.
2.1 Carbon Dioxide.
Pollack et al. (1987) have reported on detailed calculations for the surface temperature of Mars resulting from increases in CO2 up to 1000 kPa (10 bars) and for values of the solar constant equal to 0.7, 1.0 and 1.3. McKay and Davis (1991) have fitted the results of Pollack et al. (1987) with the formula
![]() (Eq.7)
(Eq.7)
where a and b are constants adjusted to give an optimum fit at 1.95 K kPa-1/2 and 2.04 K kPa-1/2 (a is not to be confused with albedo in this case) and P is the atmospheric pressure. This fit, while very accurate (see Figure 2 of McKay and Davis, 1991) is not suitable for our present purposes because it expresses the greenhouse effect as a change in surface temperature directly rather than a change in flux incident at the surface. From physical considerations the changes in temperature from various greenhouse agents are not expected to add simply. Therefore we have fit the Pollack et al. (1987) results to a parameterization of the form of Equation 3. A good fit is obtained if we let
![]() (Eq.8)
(Eq.8)
where Ptot is the total atmospheric pressure, PCO2 is the carbon dioxide partial pressure and both are in units of 100 kPa (bars). The resulting fit is shown in Figure 1 [not posted here].[This fit is as good for the S = 1 as that of McKay and Davis (1991) but is not as good for S = 0.7 and S = 1.3, systematically underestimating the effect of changes in S. Nevertheless the fit is suitable for our use here. (Statement only certain for V1.0)]
2.2 Water Vapour.
It is important to note that the effects of water vapour become important as temperatures near freezing and its greenhouse effect is no longer included in the t CO2 function, as it was in V1.0. Here, we estimate the water vapour opacity as (Kuhn et al., 1979)
![]() (Eq.9)
(Eq.9)
where PH2O is the water vapour pressure in bars given by
![]() (Eq.10)
(Eq.10)
where Rh is the relative humidity (set here to 0.7), P0 is the water vapour pressure at a reference temperature (set here to 1.4x106), L is a latent heat term (43655), R is the gas constant for water (8.314) and Ts is the surface temperature. The opacity of water vapour is thus ultimately dependent on surface temperature and is not directly modifiable within the program. The warming effect of water vapour therefore acts as a bonus to the more direct methods of climate forcing involved in terraforming.
2.3 Methane.
As Mars is being terraformed, one of the biogenic gases released might be methane. Here, the opacity of methane is estimated as (Kiehl and Dickinson, 1987)
![]() (Eq.11)
(Eq.11)
where PCH4 is the methane partial pressure in bars. In the context of Martian terraforming it is only sensible to model methane as a trace atmospheric constituent (e.g. m bar to millibar pressures).
2.4 Ammonia.
Ammonia might be produced on Mars biologically; Zubrin has also proposed importing 1 - 1000 m bars of ammonia via comet impacts (Zubrin and McKay, 1997). Here, we estimate the ammonia opacity as (Kuhn et al., 1979)
![]() (Eq.12)
(Eq.12)
where PNH3 is the ammonia pressure in bars.
2.5 CFCs.
Turning now to the CFCs, McKay et al. (1991) have calculated the surface temperature that would result from an introduction of a mixture of CFCs into the Martian atmosphere. They treated the problem by assuming that the mixture would uniformly blanket the 8-12 m m ‘window’ region of the infrared spectrum. Their results were expressed as a function of the opacity of the CFC mixture in this spectral region. They considered the addition of CFCs to the present Mars atmosphere (6 hPa CO2) and to a 100 kPa N2/O2 Earth-like atmosphere. They found that the resulting surface temperatures were similar for both cases depending only on the opacity of the CFCs in the window region. By considering these results we obtain a fit as follows
![]() (Eq.13)
(Eq.13)
where W is the opacity of the CFC mixture in this 8-12 m m window region. Equation 13 represents a good approximation to the results of McKay et al. (1991) as shown in Figure 2 [not posted here].
To express this in terms of the pressure of CFCs in the atmosphere, we need to have a value for the warming due to a given amount of CFCs. We note from Equation 4 that if t CFC is small then
![]() (Eq.14)
(Eq.14)
Here we use the results of Ramanathan et al. (1985) indicating that a mixture of CFCs such as that suggested by McKay et al. (1991) – CF3Br, C2F6, CF3Cl, and CF2Cl2 – would have a warming effect of about 0.2 K from a column mass corresponding to 1 ppb in Earth’s atmosphere. This amount of mass would be 100 m Pa on Earth and 38 m Pa on Mars. If we assume that the window region opacity is proportional to the column mass for small mixing ratio then W = g PCFC. Approximating Equation 9 as t CFC = 1.1W/50 for small values of W and combining Equations 9 and 10 we obtain the following expression for g ,
![]() (Eq.15)
(Eq.15)
where we have used dT = 0.2 and T = 288 K from the Ramanathan et al. (1985) computations for Earth. Finally, we have
![]() (Eq.16)
(Eq.16)
3.0 Climatic Equations.
Our description of the climate of Mars is still relatively small-scale and is based on the model of Zubrin and McKay, 1997.
Taking into account both greenhouse heating and advective effects, the polar temperature is taken to be
![]() (Eq.17)
(Eq.17)
where D T is what the temperature difference between the mean value and the pole would be in the absence of an atmosphere (about 75 K for S = 1).
The relation for the maximum tropical temperature is taken to be
![]() (Eq.18)
(Eq.18)
And the global temperature distribution is given by
![]() (Eq.19)
(Eq.19)
where q is the latitude, North or South.
This allows us to calculate two parameters relevant to biology. If Tt > 0, which occurs when the mean global temperature (Ts) > -25 celsius, then some part of the planet will be habitable, on the assumption that this is for those parts of Mars above freezing. From Equation 19 we can derive the latitude of the freezing isotherm
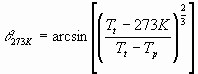 (Eq20)
(Eq20)
where q 273K is in radians.
The habitable fraction of Mars, that between q 273K N and S, is sin(q 273K), or the argument of the arcsine function in Equation 20.
It is planned soon to use these parameters, and others to be derived, in order to calculate the biological productivity of a Martian biosphere.
References.
M.J. Fogg, "A Synergic Approach to Terraforming Mars," JBIS, 45, 315-329, (1992).
Kiehl and Dickinson, "?", 1987.
Kuhn et al., "?", 1979.
C.P. McKay and W. Davis, "Duration of Liquid Water Habitats on Early Mars," Icarus, 90, 214-221 (1991).
C.P. McKay, O.B. Toon, and J.F. Kasting, "Making Mars Habitable," Nature, 352, 489-496 (1991).
J.B. Pollack et al., "The Case for a Wet, Warm Climate on Early Mars," Icarus, 71, 203-224 (1987).
V. Ramanathan et al. "Climate-Chemical Interactions and Effects of Changing Atmospheric Trace Gases," Rev. Geophys., 25, 1441-1482 (1987).
R.M. Zubrin and C.P. McKay, "Technological Requirements for Terraforming Mars," JBIS, 50, 83-92 (1997).