The superior attributes of parallel circuits has been recognised by man in computer science and artificial intelligence in the development of parallel programming, parallel distributed processing and neural networks. Are these systems at all representative of nature's informational mechanisms?

Certainly nature functions multidimensionally, and multiconnectedness has been recognised, which we model as parallel levels or strata with a hierarchical structure. But in nature, these levels, which operate nonlinearly, are not layered externally. Our current science only recognises the surface (3D) of phenomena and the external-world view of the ego, and although nonlinearity is suspected as being the basis of linearity scientists are looking for this nonlinearity externally.

It is vitally important to understand that true nonlinearity is internal nonlinearity. For instance, the third dimension of apparent linearity (but not truly) would be the first level in the strata of this internal hierarchy of spaces within spaces. As we move internally, at right angles to 3D space, we encounter changing but superimposed spacetimes. We find that 3D space has a thickness higher-dimensionally, just as an essentially 2D sheet of paper has a thickness in the third dimension.

Let us picture these internal strata as levels going up in our graphical representation. The bottom level is our familiar 3D. Now we find that this 3D has maximum focus or specificity. If we could look at an atom and move our attention inwards, that is, up the hierarchy we would find it has a higher-dimensional thickness and that it appears to expand (spiral) out and become more 'fuzzy'. We are moving from greater degrees of specificity to greater generalisation.

The concept of this generalisation would be abstract relative to our physical perceptions and 3D thinking, except that it can be interpreted as containing probabilities. That is, the probabilities are inherent within the greater 4D thickness---the generalised condition can quantum reduce from many probabilities, which by continuous selection from, say, the 3D level, reduces to one probability at our 3D level.

True parallel processing is not only the linear arrangement of networks but also includes a nonlinear arrangement underlying the first level. Note that this first level is the visible external 3D world of ego observation. Scientists are beginning to recognise the importance of nonlinearity through the study of chaos and, as we have mentioned, that it may be the basis of all linearity, but they are looking for this nonlinearity in the surface, that is, in 3D and will only find external nonlinearity---see other articles.

What will be discovered is that all separation is an illusion. We mean this in the sense that we may view mountain peaks above the surface of the ocean and consider them separate. Within the boundary given by the surface this would be true. However, if our perception is extended below the surface we will see that the mountains are joined within the body of the Earth. This would now require a more integrated science. We might wish to imagine below the ocean surface many more surfaces which continue to restrict our view but with decreasing limitation as we go down. One would then need to imagine, say, two or three peaks joining below surface 1 and connecting to another group of 2 or 3 peaks below surface 2, and so on until finally all is one in the Earth. Perception within different limitations in this way will give rise to a different physics. Consciousness evolves towards greater integrations and this invokes or mirrors the corresponding universe face or limitation.

With this model, there is only nonlinearity. But by setting different limitations (the illusions of) linear characteristics of separateness can be experienced and explored. To describe this as nature's parallel processing system is merely an attempt to describe a nonlinear system in linear terms.

As we can see, nature's parallel processing is not the same as man's linear parallel processing concept, in which man's processors are on the same level. Nature's parallel system goes inwards into higher dimensions so that each processing stratum is different. The format becomes more integrated containing more probabilities. For example, consider two levels in a company organisation, say, ground-floor workers and managers. They both are involved in the same purpose but each intrinsically requires the other. If the workers correspond to energy units of the third dimension, then the managers are energy units/oscillations acting 'parallel' but slightly higher dimensionally (of higher frequency). Now whereas the workers express one probability the managers will contain numerous probabilities governed by the boundary conditions of the product, species, etc., whatever is being expressed. However, it is the ground-floor workers who select the requirements and the single probability at the 3D level.

The geometry and frequency of the energy must be quantum reduced on a gradient from 'president' to ground-floor workers through countless stages of 'executives' to 'managers', etc. until the energy 'fits' in the third dimension and obeys the laws of the third dimension. It doesn't have to, but our left-brain consciousness will demand it and consequently select it.

Even transmissions of information (bodies) by teleportation would be totally nonlinear (not the crude and dangerous explanation in the linear method depicted in the Star Trek series). There are no true breaks in energies or localities of apparent separation. All parts ultimately are joined at some level but by having levels of limitation (for example, not able to, say, utilise the levels above one's own stratum of existence), 'temporary' individual characteristics can be explored and the knowledge retained (and shared ) within the whole (and we have unintentionally described the God concept).

If our civilisation wasn't programmed and negatively influenced to believe and teach that existence evolves from the 'bottom-up', that is, the Darwinian approach, it would equally well consider the 'top-down' theory. And this latter view would be the one that would account for the various mysteries in science: chaos, fractals, quantum reduction, religion, nonlinearity, etc. In the 'top-down' theory we have the potential for the God concept; it is the creationist approach to life (see other articles). This theory will reveal a proper understanding of nonlinearity.

We might ask the question, How would one create linearity from nonlinearity? (Everything seems to be basically linear in our space and time world.) We would begin with one whole quantum state and start the process of division, that is, increasing fractionalisation; each further division would create a lower frequency. However, this process would be meaningless without setting limitations, otherwise a fragment would 'know' it was from the whole and would thus identify with the whole and nothing would be gained. It is essential that at each level of division there is an inherent barrier which prevents the lower-level (lower frequency energy) 'knowing' about the upper levels. Use the analogy of the mountain peaks above the ocean, given above. These boundaries will now enforce separation (owing to absence of knowledge of their higher connection) and create linearity. There would thus be different degrees of linearity at the different levels of frequencies and limitations.

Now the different 'parallel' levels will have information stored in a different format (different framework, different dimensions). Any level of existence in this hierarchy must cooperate with the levels above (e.g., the managers can't communicate adequately to the president, they must go through the executives to achieve the correct formatting of information for the communication). One level is useless on its own and it can't utilise other levels without transduction on a gradient (see other articles) between levels. For instance (and we have given this example before), in moving the hand/arm from A to B (picture, say, a one-foot horizontal movement) there are many parallel levels within the learning pattern for this movement. At one extreme (the 'top' of the hierarchy) it is one quantum state, which is useless for coordination unless it teleports the hand from A to B. And at the 'bottom' of the hierarchy we have a very linear situation in which minute information bits can be pictured in a long line for action over this distance, A to B. All the countless levels between these two extremes are necessary otherwise chaos will result.

 In summary, linear systems can never duplicate nature. With the introduction of higher-dimensions, internal nonlinearity can be recognized and interpreted as a 'strata' of parallel processes. As described in other articles the internal structure is (higher-dimensionally) holographic and holistic giving a field of coverage in the linear plane of the third dimension, in which processes are related in a linear-parallel-processing manner but based on their internal connection (nonlinear parallel processing). In effect, different quantum states are simultaneously impinging ('down') into the third dimension, giving the reasons and mechanisms for the relationship amongst all phenomena. (Note that this hierarchical mechanism is telling us that there is one whole, from which a series of divisions are projected, with barriers between these divisions, forming the nature of all things---see article The Theory of One.)

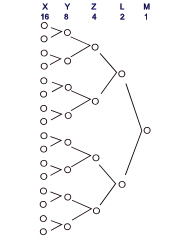
We have explained how linearity can be arrived at from nonlinearity. Let us now consider how we might create nonlinearity from linearity. The computer programmer might wish to imagine a complex loop system. Firstly, consider a single array---this demonstrates linearity; a single line or stratum. For the sake of illustration let us give this array 16 address locations for storage and operational information. This is the X array, which has 16 elements.

And we have,

X = 1 to 16

This might correspond to a string of information for a physical movement in a skilled action, except that scientists have recognised that it is hardly likely to be linear (in skills), that is, having countless linear sequences stored in the mind for different movements. Thus 1 to 16 is 100% linear. The purpose is to change it to 100% nonlinear. Let's improve it at the next step. We begin by putting X = 1 to 2.

We now add another dimension Y, giving it an array of 8 elements, since although we are gradually converting from 16 linear-operated locations to a first degree of nonlinearity the 'mechanism' must still create the 16 locations or states. Thus Y will be 8, and X = 1 to 2 (8 looped twice gives 16).

And we have,

X = 1 to 2
Y = 1 to 8

The linearity degree has reduced from 16 to 8 and non-linearity has increased from the first level X or dimension to the second one Y.

We now take it a further step and construct the third dimension Z---a further degree of nonlinearity. We now put: Y = 1 to 2, and Z = 1 to 4 (4 looped twice, looped twice again gives 16).

That is,

X = 1 to 2
Y = 1 to 2
Z = 1 to 4

This is still a partially linear system, that is, there is still a string of 4 states.

Next we add a fourth dimension L. The values are now: Z = 1 to 2, and L = 1 to 2 (2 looped three times gives 16).

That is,

X = 1 to 2
Y = 1 to 2
Z = 1 to 2
L = 1 to 2

This means only two elements are linearly presented but they can manifest 16 different states. That is, the degree of linearity is 2. It needs to be unity.

As a final touch and completion of the convergence to nonlinearity we add a fifth dimension, M (=1), necessary to unify the whole dimensional array at the location L = 2. Thus 16 separate X states are now operated by 1 M state. The states Y, Z, L, M are nested within the 16 X states, and give 16 possibilities to the operations. This is a simple structure demonstrating how, for instance, a learning pattern functions in physical skills. See articles on skills.

Return to Home Page