
In the article I said that Archimedes was investigating pi by inscribing and circumscribing circles with regular polygons, but what does this involve?
If we take the area of a circle to be pr² then if we can calculate the radius and area of a circle we would know what pi was.
We could draw a circle, place a grid over it, count the number of squares across the circle and the count the number of squares inside the circle and you can see what to do next. But this would only obtain a certain degree of accuracy.


How about doing this using algebra? if we drew a shape around the outside of the circle, which we could calculate the area of, and drew a shape around the inside of the circle, which we knew the area of then we would have a lower and upper bound for the area. Take the example of a radius of 1, therefore the area is pi. If we then inscribed the circle with a triangle and calculate the area of the triangle we would have a lower bound for pi.
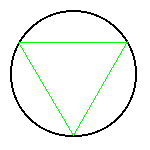 | The triangle is inside the circle, therefore the area of the triangle is less that the area of the circle. We know that the area of the circle is pr², we also know that the area of the triangle is ½bh. if we fix the radius at 1, then the area of the circle is p and p > ½bh |
In a similar way we can fix an upper bound for pi:
The triangle is outside the circle, therefore the area of the triangle is greater that the area of the circle. We know that the area of the circle is pr², we also know that the area of the triangle is ½bh. if we fix the radius at 1, then the area of the circle is p and p < ½bh | 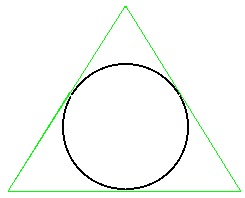 |
Now, if we had a regular polygon with n sides (a n-gon) we could split it in to n identical isosceles triangles, the area of each one can then be calculated to find the total area.
For Example:
Using the same images as before (triangles therefore n=3), we can split the polygon in to n isosceles triangles. The middle angles add up to 360º, so each one must be 360 / n.
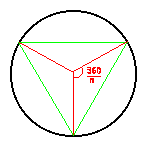
If we take just on of these isosceles triangles (radius of the circle still 1) then using trig. we can calculate the area.
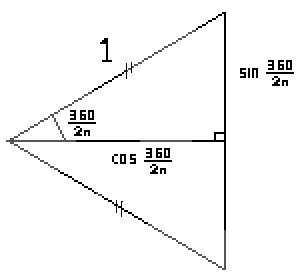
Now the base length is 2 sin (360 / n) and the height is cos (360 / n), so the area is ½ × 2 sin (360 / n) × cos (360 / n) which equals sin (360 /n) × cos (360 / n) which equals (this is a strange but true fact and you'll just have to believe me) ½ sin (360 / 2n). So that works for inscribed polygons, what about circumscribed polygons?
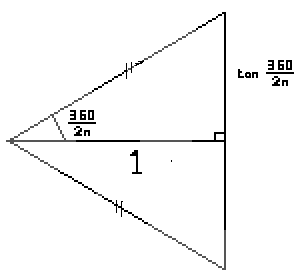
Here the base length is 2 tan (360 / n) and the height is 1 so the area is ½ × 2 tan (360 / n) × 1 which equals tan (360 / n).
So hows about plotting these?
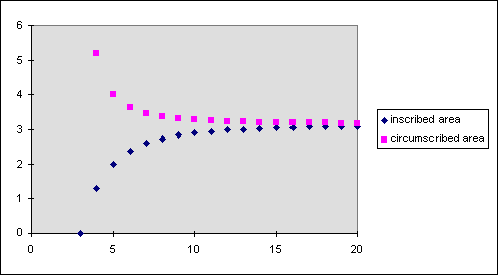
Here the x-axis is the number of sides on the polygon, and the y axis is the area of the polygon, derived using the two equations above. As you can see the values converge to a single value, which is pi. Archimedes continued this up to 96 sides, which gave him value for pi to 3 significant figures.
This may all seem very strange, but a similar item occurs in "Problem Solving" on case study 10, this time the ideas are based on the perimeter of a circle lieing between that of circumscribed and inscribed regular polygons.
Credits: written by Luke Wakeling