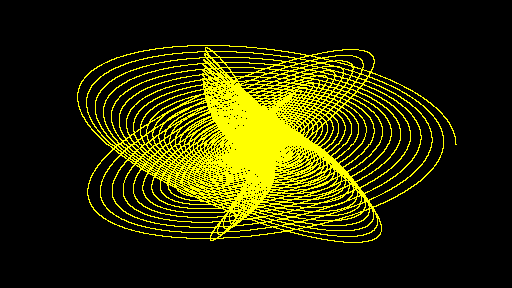
A computer simulation of a harmonograph.
William Overington
Copyright 2001 William Overington
Monday 23 July 2001
This document is a case history of preparing web based simulations of a computer simulation of a mechanical instrument.
Many years ago in a magazine I read an article about a mechanical instrument called a harmonograph. I was fascinated. As best I remember the harmonograph consisted of a frame of the size of about a metre tall by about half a metre wide by one and a half metres long.
There were located within the frame a short distance from each end two rigid rod pendulums, each of which had an adjustable cylindrical weight that could be raised or lowered on the rod between runs, thereby altering their frequencies of swinging.
One of the pendulums was in a universal joint of some sort and above the joint on the upper end of the rod was a flat plate, upon which a sheet of paper could be fixed. Let us suppose that the paper was about A4 in size.
The other pendulum was in a one dimensional joint and above the joint on the upper end of the rod was a one degree of freedom joint to another rod, to the other end of which was attached a pen.
The harmonograph was run by fixing a clean sheet of paper onto the flat plate, then pulling the lower end of the first pendulum away from vertical, then pulling the lower end of the second pendulum away from vertical, placing the pen onto the paper and letting go of both pendulums at once, giving the pendulum with the universal joint a sideways push.
Gradually the motion of both pendulums decays and a drawing is produced.
Several such drawings were reproduced in the article.
In the simplified mathematical model of the harmonograph in this document I have treated the flat plate that carries the paper as always being horizontal, when in the real mechanical instrument, apart from when the pendulum upon which the flat plate of the harmonograph is mounted has come to rest or for perhaps a split second from time to time during the operation of the instrument, it is not horizontal. Also, in the simulation the pen is always on the same horizontal line, in one horizontal plane, when in the real instrument it will have some vertical motion as it rides on the surface of the flat plate.
However, in qualitative terms, these simplifications seem to have no great effect. The designs produced by this computer simulation are consistent with my memory of the illustrations that were in the original article in the magazine.
In designing this mathematical model I have simply applied motion to a drawing point. I have not modelled the fact that the paper is moving and the pen is moving and subtracted the position of the paper from the position of the pen to get the position of the drawing point.
My mathematical model is that a drawing point has a circular motion in a plane and in addition has a sinusoidal motion along the horizontal axis.
I use the parametric equations of the motion with time as follows.
x = cos (at) e-t/p + cos (bt) e-t/q
y = sin (at) e-t/p
With the convention that x and y are on the mathematical plane with x increasing to the right and y increasing upwards, together with X and Y are on the computer screen display with X increasing to the right and Y increasing down the page, and X0 and Y0 being the coordinates of the centre of the display area, I use the mappings below to display the results of the simulation.
X = X0 + (100 * x)
Y = Y0 - (100 * y)
However, in the software I use xdisplay instead of X and ydisplay instead of Y as although case is significant in Java programs, I try to distinguish between identifier names by more than just letter case.
For the half scale simulated DVB-MHP display that I am using in this program, the 100 is a good scaling factor for the display. The value of X0 is 256 and the value of Y0 is 144. As x can move between values of -2.0 and +2.0, X can move between 56 and 456. As y can move between values of -1.0 and +1.0, Y can move between 44 and 244.
On a full size 1024 pixel by 576 pixel large screen, wide screen 16:9 format DVB-MHP terminal the display, scaled up by a factor of 2 in each direction, gradually drawing a display over about a minute or so, might look quite spectacular and eye catching.
I begin by generating a file ast00801.java as a copy of the file ast00701.java that I used in the arithmetic questions program in the "Programs producing questions about arithmetic." document. I change the name of the class to become ast00801 and change the date.
Firstly I shall take out those parts of the copied program that relate to the application program within the ast00701 program, so as to leave a simulation of a DVB-MHP terminal that has activated buttons and mouse capability, yet having no application program simulated as running upon it.
This ast00801 program does not use a mouse. However, I shall leave all of the mouse simulation capability in the simulation parts of the program.
I shall also leave the part where the application tests for whether there is a mouse attached to the particular simulated DVB-MHP system. This may not be necessary, but I have left it in so as to provide for the possibility that this software might be adapted to some later program and so it will be clearer as to how the question of whether a mouse is attached to the DVB-MHP terminal is determined.
My intention is to have two screen displays. The program starts with screen display 1. Data is entered using the digit buttons, the particular parameter that is being entered being selected using the red and green buttons. The numbers can be cleared using the blue button.
In order to simplify the program parameters are entered as integers and values are divided by 1000 before they are used.
The ratio of a to b is the key factor that determines the shape of the drawing produced rather than absolute values.
The program has default values added, which I found after some experimentation as being a set of numbers that provides a reasonable display.
When the data has been chosen as the user desires, the user pushes the yellow button and the screen is cleared and a simulated harmonograph drawing is produced in yellow, taking a while, perhaps several minutes, to draw, depending upon the speed of the terminal being used.
This slow drawing has been achieved by including a loop which computes one thousand random numbers (yet not using them) for each line segment on the drawing, just to slow the drawing down due to the huge number of random numbers being produced. The speed of drawing may vary from terminal to terminal due to the possible variation of speed of the microprocessor hardware between one terminal and another terminal. There is a method using the system clock that could be used in order to make sure that the program waits for time and that method could make the program run at the same speed on all terminals that could keep up with the relatively slow minimum processor speed that would be needed to maintain the speed of drawing desired on the screen. However, in this scenario of simulating a DVB-MHP system on the web that method is not used. If this program is converted to run on a DVB-MHP terminal and is broadcast, maybe an improved version that locks onto the system clock can be produced at that time.
This simulation works well and fun can be obtained by entering different sets of numbers on screen 1 and observing the drawings.
On a PC the drawings can be saved onto the clipboard using the Print Screen button and then using paste in a drawing program such as paint and then trimming around the edges. Some diagrams made using this technique are included in this document. Some of them are made using the modified program where there is a choice of pen colour.

a=1000 p=300000 b=1330 q=300000
the default values
Attention is now turned towards modifying this ast00801 program to produce the ast00802 program where there is a choice of pen colour in which the drawing is made. The process of producing the ast00802 program from the ast00801 program has a number of fascinating aspects.
Firstly, the display screen 2 is renumbered as display screen 3 and a new display screen numbered as 2 is introduced.

a=500 p=300000 b=1520 q=300000
Please note how once the program moves into display screen 2, pushing the colour buttons has no effect and that pushing the digit buttons has a different effect than for pushing a digit button when the program had display 1 on the screen.
Perhaps the biggest difference in the ast00802 program from the ast00801 program from which it is derived is that the piece of software that draws the picture is moved from within the section that responds to a push of the yellow button into the section that responds to a push of a digit button.
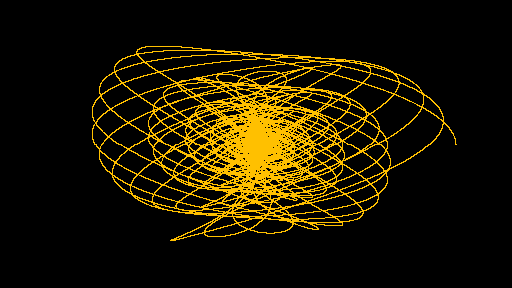
a=500 p=300000 b=950 q=300000
The ast00803 program is a testing version of the ast00802 program and was used to determine the value up to which the variable i would count by experimentation as to for how long the program needed to compute in order to get a settled display for various choice of parameters. In fact, once a suitable value was found, ast00801 and ast00802 were both adjusted to that value.
The ast00804 program is a version of the ast00802 program that has had the delay loop removed. It is useful for experimenting with looking at the effects of varying the parameters upon the drawing that is produced.
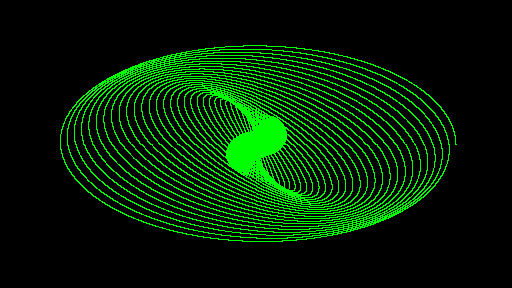
a=630 p=300000 b=640 q=300000
Here are links to viewing the web based simulations. A Java enabled browser is required.
The web based simulation of a computer simulation of a harmonograph.
The web based simulation of a computer simulation of a harmonograph, with choice of pen colour.
Links to full listings of the first three programs follow, together with a note about the small changes made in a copy of the source of the ast00802 program to produce the source of the ast00804 program.
Here is the piece of source code that was removed from a copy of the source code of the ast00802 program in order to produce the source code for the ast00804 program for the computer simulation of a harmonograph, with choice of pen colour, with no delaying loop. Apart from the change of class name from ast00802 to become ast00804 this is the only difference between these two programs.
// delay loop so that the picture draws slowly on the screen
for(int j=0;j < 1000;j++)
{
double r;
r=Math.random();
}
The harmonograph program provides Astrolabe Channel with a program that provides a changing screen display over a period of time and which, once it were converted to DVB-MHP format, might be particularly suitable for a demonstration on a stand at an exhibition concerning the DVB-MHP system.
In particular please note that the program uses the polyglot compatibility section technique, so versions of these programs for languages other than English, such as German, Finnish and Norwegian could be produced straightforwardly. There is not much use of words in this program and perhaps that might well make these programs useful as a demonstration of producing versions of one program in a variety of natural languages as well as being an eye catching display of mathematical interest.
Astrolabe Channel
Copyright 2001 William Overington
This file is accessible as follows.