Random Walk, An Introduction
A Tilemodule by William Overington
[ This is the first tilemodule that I have authored for the internet. It is thus of research interest in the assessment of tilemodules as a method of distance education, as well as being a learning package. The topic, though a specialized mathematical technique, is straightforward for people without a mathematical background to understand. The potential to be suitable for a wide audience interested in the future of distance education on the internet is a key factor in its choice as the topic for this tilemodule. ]
Please know that a complete list of filenames for this tilemodule, expressed as hyperlinks, is at the bottom of this document so as to assist any students who wish to download this tilemodule to local storage for off-line study.
This tilemodule introduces the mathematical technique of random walk. Random walk can sometimes be suitable for tackling extremely complicated problems that cannot be readily solved by other methods. However, the technique can also be used to solve very straightforward problems that can be solved by other methods. This may be inefficient in terms of the time taken to solve the problem, but can be useful as a calibration process for the complicated problems.
In this tilemodule the technique of random walk is explained using a very simple problem. A learner will be able to attempt to solve such a problem by using the random walk method.
In order to complete this tilemodule you will need the following.
Pen and paper.
A coin to flip, one side known to you as head and the other as tail.
An item, hereinafter called the chess piece, to place and move around on some squares drawn on a piece of paper.
The physical situation
Imagine a wall, like the wall of a house. This wall is one unit in thickness at all places, it does not matter what that unit is in this problem. The wall is solid all the way through and made of uniform material. In addition this is a very mathematically convenient wall as it is infinitely high and infinitely wide. The temperature outside the building is 5 degrees Celsius and the temperature inside the building is 25 degrees Celsius. There are no draughts and this situation has existed for a very long time so that the temperatures will all have settled down to steady values. This is called a steady state problem. This is just a convenient way of saying that when we wish to consider the temperature at a point inside the material of the wall for the purposes of this learning package on the random walk technique we are making every simplifying assumption that we can make in order to keep it simple. When these simplifying assumptions, or even just some of them, cannot be made, then the problem gets more complicated. Problems related to such situations can sometimes be solved using the random walk method where other techniques are unsuitable.
Let us choose to consider the temperature at five points. These are on a straight line directly through the wall, which is perpendicular to both surfaces of the wall. The five points are a point on the inner surface of the wall, a point half way between the inner surface of the wall and the centre of the wall, a point at the centre of the wall, a point half way between the centre of the wall and the outer surface of the wall, a point on the outer surface of the wall.
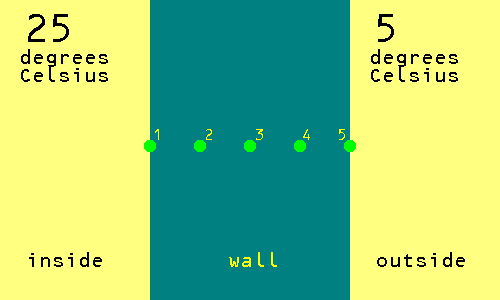
We now draw a board game like diagram as shown below.
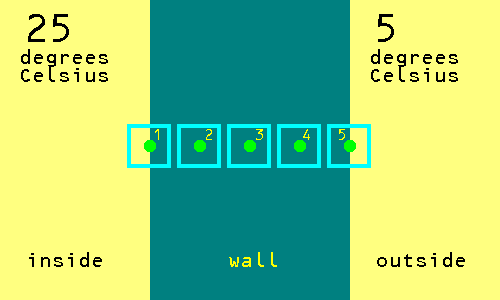
First Stage
Let us make a first random journey.
Place the chess piece on the point labeled 3, that is the centre of the wall.
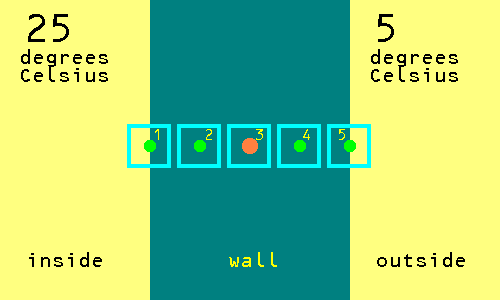
Flip the coin. Let us suppose that it is a head. In that case move the chess piece one square to the right.
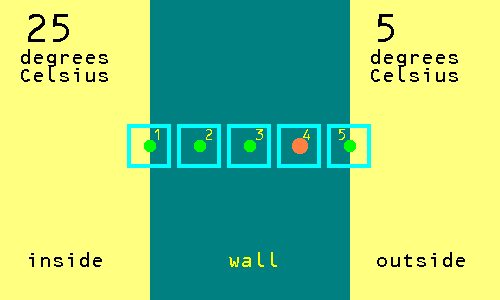
Is it on a square with a temperature? No. So flip the coin again. Let us suppose that it is a head. Move the chess piece one square to the right.
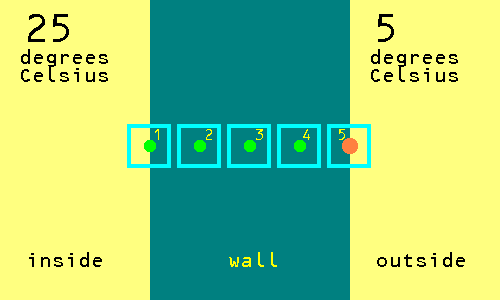
Is it on a square with a temperature? Yes. So stop this journey. The temperature is 5 degrees Celsius so we add 5 to a running total. The total so far is 5 as there was nothing in the running total when we started. Without altering the running total, make a copy of the running total and divide it by the number of journeys so far completed, which means to divide by 1 this time. So, our first estimate of the temperature at the centre of the wall is 5 degrees Celsius. Now, the situation is that the correct answer is 15 degrees Celsius at the centre of the wall. At the point nearer the inside the correct answer is 20 degrees Celsius. At the point nearer the outside the correct answer is 10 degrees Celsius.
So let us get a better estimate. We again place the chess piece on the point labeled 3, that is the centre of the wall.

We carry out a second journey in much the same way as before, except that this time the running total does not start at zero but starts at whatever was the result from the first journey. This happened to have been 5 degrees Celsius, but could have been 25 degrees Celsius. Flip the coin. Let us suppose that it is a head. Move the chess piece one square to the right.

Is it on a square with a temperature? No. So flip the coin again. Let us suppose that it is a tail. Move the chess piece one square to the left.

Is it on a square with a temperature? No. In fact it is back at the centre of the wall. This is no problem, we must just keep flipping the coin and moving the chess piece accordingly, right for head, left for tail, until a square with a temperature is reached. Note that this right for head, left for tail movement is my own convention, it is not a fixed rule of the random walk method. The random walk method will still work however one relates the coin side to the movement as long as it is the same all through. One needs to devise such conventions in order to make the method work. Let us suppose that two heads then occur in succession so that the temperature on the square at which the journey ends is 5 degrees Celsius.
We will have had

and then

to complete the journey.
The running total is now 10, there have been 2 journeys and so the second estimate for the temperature at the centre of the wall is 10 divided by 2, which is 5 degrees Celsius.
Let us imagine a third journey. Again we place the chess piece on the square labeled 3.

Flip the coin. It gives tails. Move the chess piece one square to the left. This is to the square labeled 2.
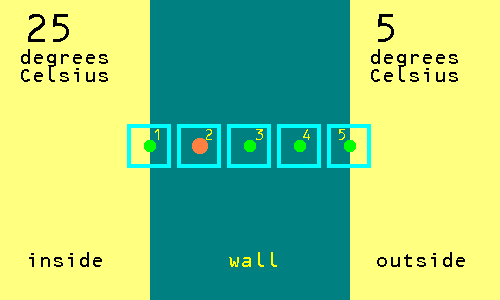
Is the chess piece on a square with a temperature? No. So flip the coin again. Let us suppose that it is a tail. Move the chess piece one square to the left.
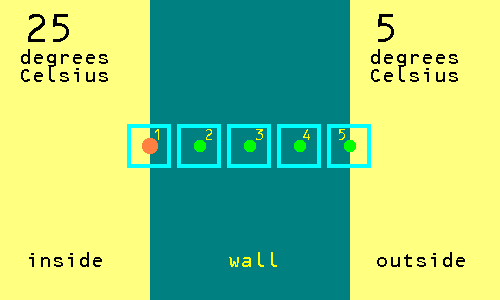
Is it on a square with a temperature? Yes. So stop this journey. The temperature is 25 degrees Celsius so we add 25 to a running total. The total so far is 35. The running total is now 35, there have been 3 journeys and so the second estimate for the temperature at the centre of the wall is 35 divided by 3, which is 11.33 degrees Celsius.

Perhaps you would like to try a random walk journey yourself now. Draw a table of results as shown in the diagram above and copy down the results of the first three journeys as are also shown in the diagram above. The first three journeys are made up so as to produce a selection of short journeys so as to help in explaining the principle of random walk to you. Your actual journeys in this simulation may be two, four, six or some larger even number of steps long. Sometimes you may get a journey with many steps. Place the chess piece on square labeled 3, that is the centre of the wall.

This is journey 4. Flip the coin. If it is a head, move the chess piece one square to the right ; if it is a tail, move the chess piece one square to the left. You will not have landed on a square with a temperature on it, so flip the coin again and move the chess piece accordingly. Now I can no longer know whether the chess piece is back at the centre of the wall or at one of the two surfaces. It is for you to now complete journey number 4 and produce a fourth estimate for the temperature at the centre of the wall. Enter the journey in the table of results as you proceed. When the journey ends, calculate a fourth estimate for the temperature at the centre of the wall.
Next carry out a fifth journey and produce a fifth estimate for the temperature at the centre of the wall. Carry on until you have carried out ten journeys.
Second Stage
Now try to solve a different problem on your own using the same random walk technique. The problem is to find the temperature at the point labeled 2 by a random walk method. Start a new table of results with the journey number starting at journey number one and the running total starting at zero. For this problem, start each journey with the chess piece on the square labeled 2.

If the first flip of the coin gives a tail, then you will have completed the journey after one flip of the coin. You cannot complete the journey to finish at the outside surface of the wall with less than three flips of the coin. It is now much more likely that the journey will end at the inside surface of the wall than at the outside surface of the wall. This means that the temperature that you calculate will be much nearer to 25 degrees Celsius than to 5 degrees Celsius, which is correct. Notice that in this simulation the number of steps in a journey will be one, three, five or some larger odd number of steps long.
Third Stage
Now we can try the same steady state temperature problem so as to get the temperature one tenth of the way into the wall from the inner surface. This time we need a new board game like diagram with eleven squares.
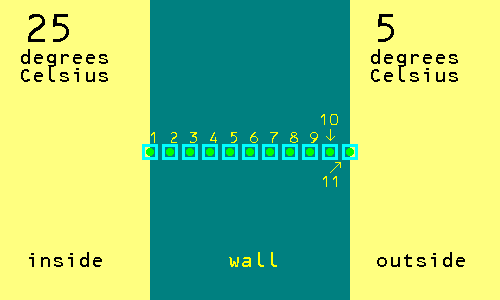
The correct answer is 23 degrees Celsius. Start a new table of results with the journey number starting at journey number one and the running total starting at zero. Start each journey with the chess piece in the square labeled 2.
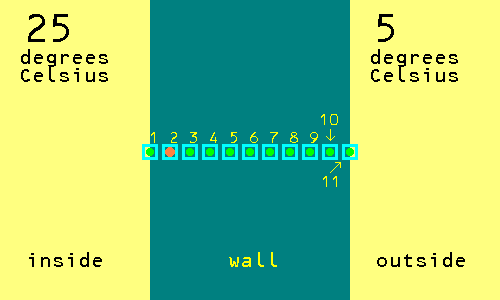
Flip the coin. If it gives a tail, then the journey is finished.
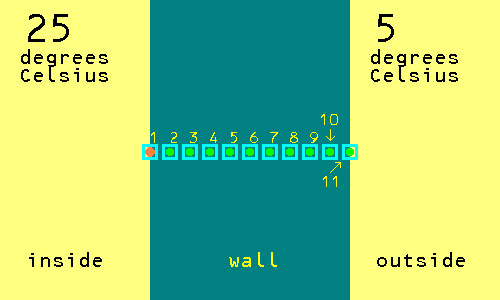
If it gives a head, then the journey will continue.
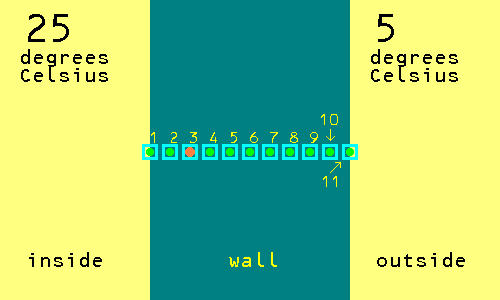
It may take a long time for the chess piece to reach one of the two surfaces. In fact it may take so long to reach a surface that, once you have flipped the coin about twenty times it is of no educational benefit to you to keep trying to solve the problem by hand. As long as you carry out about twenty flips you should have got a feel for the way that the journeys take a lot longer when the steps are smaller.
Please be aware that the random walk journeys that you have carried out by hand can be carried out by computer. It takes time to write a computer program to simulate the random walk journeys, yet once written thousands of journeys with many random steps in each can be carried out quickly.
To complete the tilemodule save all your documents for this tilemodule in your portfolio.
For the convenience of students who wish to copy all of the files of this tilemodule to their own local storage, here is a list of the files as hyperlinks.
rwai0001.htm this text file
rwai0000.gif graphics file
rwai1000.gif graphics file
rwai1001.gif graphics file
rwai1002.gif graphics file
rwai1003.gif graphics file
rwai1004.gif graphics file
rwai1005.gif graphics file
rwai2000.gif graphics file
rwai2001.gif graphics file
rwai2002.gif graphics file
rwai2003.gif graphics file
rwai3000.gif graphics file
rwai9000.gif graphics file
9 February 1998
End of document