Your Spectrum
Issue 4, June 1984 - Plotting in 3D (part 2 of 2)
Home Contents KwikPik


See also this other article in the series:
Issue 3part 1: "Graphics & Mathematics"
This program is available on "ZIPi'T'ape",
which holds the files for both parts of the article.


In Part One (published in last month's Your Spectrum), the perspective was demonstrated using the 'plane plotting' routine. This time, the spherical co-ordinates are chosen to generate a variety of symmetrical 3D objects and also to provide relatively simple transformations (scaling, rotation and translation). 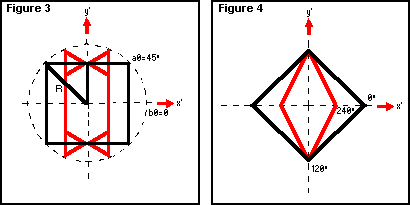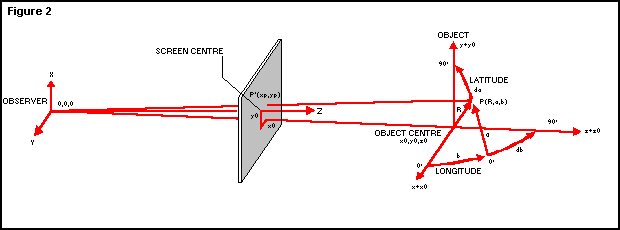The routines are used in the main part of the program (listed in Part One) and the co-ordinates system is depicted in Figure 2.
  Object generation starts at line 90 with the set of INPUT statements defining object parameters chosen by the observer. The parameters asked for in the program will produce data for the generation of:

- the number of vertical sections, sb
- the number of sides in each section, sa
- the starting longitude; that is, the longitude bf the first vertical section, b0
- the starting latitude; that is, the latitude of the origin of the DRAW vector representing the first side of the polygon, a0.
This can be seen in Figure 3.
sb = 3
sa = 4
b0 = 0
a0 = 45°

Figure 3 will generate three vertical sections - at 0°, 120° and 240° - each section being represented by a wire- frame figure of a square orientated so that it has two horizontal and two vertical sides. If you were to make a0 equal to 0°, you would produce squares with sides at 45° to the horizontal (see Figure 4).
  The object size will obviously be determined by R (line 100) and the apparent size using perspective will also depend on the object distance from 		title
Continuing on his quest to make perspective a reality on the Spectrum, Damir Skrgatic tackles the subject of symmetrical figures generated through the application of spherical co-ordinates.
the observer, z0 (line 90). Varying the value of z0 is equivalent to 'zooming' with a camera - translation along depth. The x and y translation is achieved by varying x0 and y0 respectively (the centre of the screen is x0=0 and y0=0).
  So now, with reference to the 3D Plotting program published in the first part of this article (see last issue), here follows a detailed breakdown of the 		lines which deal specifically with spherical co-ordinates.
  Lines 170 and 180 convert chosen numbers, sb and sa, into angular increments in degrees, db and da, used by the FOR-NEXT loops in lines 190 and 200.
  Lines 210 to 270 convert spherical co-ordinates R, a and b into rectangular co-ordinates x, y and z (and their increments: dx, dy and dz), so that the object
Figures 3 & 4
Figure 2

small title
can be plotted in perspective in a similar manner to the plane drawing routines demonstrated in Part One.
  Lines 220 to 240 are standard equations converting spherical co-ordinates into rectangular co-ordinates and can be derived from Figure 2 using trigonometry. (Note that all angles under SIN and COS have been converted to radians = PI/180 * angle in degrees.)
  Lines 250 to 270 compute cartesian increments (vectors) dx, dy and dz, corresponding to the latitude increment, da. (This is a good example of a very cumbersome number crunching exercise which a home computer can do easily, although not as fast as CAD dedicated machines.) Note that all results are still in millimetres.
  Lines 280 to 360 provide clipping outside the viewing pyramid and the 		FURTHER PARAMETER EXAMPLES FOR THE 3D PLOTTING PROGRAM*
With translation along the x-axisWith translation along the z-axis ('zoom')
z0
R
x0
y0
sb
sa
b0
a0 		800
60
 
0
1
4
90
45 		700
60
 
0
1
4
45
45 		 
60
50
0
2
3
0
0 		 
30
-50
-31
1
4
0
45 		 
20
-50
31
1
8
90
0
*These parameter examples are to be used in conjunction with the 3D Plotting program published in the last issue of Your Spectrum.
limits used correspond to d = 500mm and the Spectrum screen window size as measured on a 12-inch TV (see Part One).
  Line 370 is the standard perspective transformation (Equation 1) used in the subsequent PLOT statement in line 380. Note that millimetres are converted into pixels in line 380.
  The expression at line 383 has already been mentioned in the 'floor' subroutine in Part One; dk represents the decrement of scale factor (d/z) when the 		depth increases by dz. Line 390 is rather more complicated than we have met so far and as such is fully explained in the Appendix under 'vector' projections.
  It'll suffice here just to explain the combined role of two different terms which make up dxp:
- dx * d/z is the perspective component due to an increase in the vector, dx
- x * dk is the perspective component due to the vector, dz
- dx * d/z is the perspective component due to an increase in the vector, dx
- x * dk is the perspective component due to the vector, dz
The role of dyp can be explained in a similar fashion.
  Line 410 draws the perspective projection of a combined vector due to dx, dy and dz, in pixels. Lines 420 and 430 complete the FOR-NEXT loops for latitude and longitude stepping. Line 440 jumps to the beginning of the main program, asking for parameters of the next object to be drawn.
  A few examples of modelling with spherical co-ordinates to form 'objects' were given in the first part of this article. Following the explanation of how objects are generated, here is a more comprehensive list of parameters - and their effects. For reference, see Figures 1 and 2, and lines 100 to 160 of the 3D Plotting program featured last issue:
1. Select the figure type using the variable, sa
sa=1 - this draws a point in space
sa=2 - this draws a line in space
sa=3 - this draws a triangle in space
sa=4 - this draws a square in space
sa=5 - this draws a pentagon in space
When you substitute a value of more than 15 for sa, you find that a circle is drawn in space.
2. Determine the figure orientation with the starting latitude, a0, in degrees.
a0=0 - the first (and last) figure apex on the equator
a0=45 - the first (and last) figure apex at latitude 45°
3. Select the number of vertical figures (sections), sb, starting at longitude, b0, where:
b0=0° - draws the first (and last) figure in the plane z=z0 - that is, 'head-on' parallel to the screen.
3D PLOTTING
A modified version of last month's listing. If you want to update, look at lines 70-80, 430 and 660-1000.
 10 REM Wire frame objects in           perspective. D.SKRGATIC
 20 GO SUB 440: STOP
 30 PRINT AT 21,13;"Y=-62mm";AT 11,26;"x=90mm";AT 0,13;"y=62mm";AT 11,0;"x=-90mm"
 40 LET p=1.41
 50 LET d=500
 60 GO SUB 510
 70 INPUT AT 0,0;"Plane intersection:v or h";a$
 80 IF a$="h" THEN GO TO 660
 90 INPUT "Eye-object dist. in mm,z0=";z0
100 INPUT "Object 'radius' in mm,R=";R
110 INPUT "Obj. cent. offset in mm,x0=";x0
120 INPUT "y0=";y0
130 INPUT "Numb. of vert. sections,sb=";sb
140 INPUT "Num. of sides,each sect.,sa=";sa
150 INPUT "Start. longitude in deg.,b0=";b0
160 INPUT "Start. latitude in deg.,a0=";a0
170 LET db=360/sb
180 LET da=360/sa
190 FOR b=b0 TO 360+b0 STEP db
200 FOR a=a0 TO 360+a0 STEP da
210 LET x=R*COS (PI/180*a)*COS (PI/180*b)+x0
220 LET y=R*SIN (PI/180*a)+y0
230 LET z=R*COS (PI/180*a)*SIN (PI/180*b)+z0
240 LET dx=R*COS (PI/180*b)*(COS (PI/180*(a+da))-COS (PI/180*a))
250 LET dy=R*(SIN (PI/180*(a+da))-SIN (PI/180*a))
260 LET dz=R*SIN (PI/180*b)*(COS (PI/180*(a+da))-COS (PI/180*a))
270 IF x>z/5.6 THEN LET x=z/5.6
280 IF (x+dx)>z/5.6 THEN LET dx=z/5.6-x
290 IF y>z/8.3 THEN LET y=z/8.3
300 IF (y+dy)>z/8.3 THEN LET dy=z/8.3-y
310 IF x<-z/5.6 THEN LET x=-z/5.6
320 IF (x+dx)<-z/5.6 THEN LET dx=-z/5.6-x
330 IF y<-z/9 THEN LET y=-z/9
340 IF (y+dy)<-z/9 THEN LET dy=-z/9-y
350 LET xp=x*d/z: LET yp=y*d/z
360 PLOT xp*p+128,yp*p+87
370 LET dk=d/(z+dz)-d/z
380 LET dxp=dx*d/z+x*dk: LET dyp=dy*d/z+y*dk
390 LET e=ABS ((z-d)/200)
400 DRAW INK e;dxp*p,dyp*p
410 NEXT a
420 NEXT b
430 GO TO 70
440 PLOT 0,0
450 DRAW 255,0
460 DRAW 0,175
470 DRAW -255,0
480 DRAW 0,-175
490 BORDER 5
500 RETURN		 510 FOR z=d TO d+600 STEP 100
520 FOR x=-90 TO 90 STEP 22.5
530 LET xp=x*d/z
540 LET yp=-62*d/z
550 LET f=INT ((z-d)/200)
560 PLOT xp*p+128,yp*p+87
570 LET dk=d/(z+70)-d/z
580 DRAW INK f;x*dk*p,-62*dk*p
590 PLOT xp*p+128,yp*p+87
600 LET dxp=20*d/z
610 IF x+22.5>90 THEN LET dxp=0
620 DRAW INK f;dxp*p,0
630 NEXT x
640 NEXT z
650 RETURN
660 INPUT "Eye-object dist. in mm,z0=";z0
670 INPUT "Object radius in mm,R=";R
680 INPUT "Obj. cent. offset in mm,x0=";x0
690 INPUT "y0=";y0
700 INPUT "Numb. of sections,sa=";sa
710 INPUT "Num. of sides,each sect.,sb=";sb
720 INPUT "Start. longitude in deg.,b0=";b0
730 INPUT "Start. latitude in deg.,a0=";a0
740 LET db=360/sb
750 LET da=360/sa
760 FOR a=a0 TO 360+a0 STEP da
770 FOR b=b0 TO 360+b0 STEP db
780 LET x=R+SIN (PI/180*b)+x0
790 LET y=R*COS (PI/180*b)*SIN (PI/180*a)+y0
800 LET z=R*COS (PI/180*b)*COS (PI/180*a)+z0
810 LET dx=R*(SIN (PI/180*(b+db))-SIN (PI/180*b))
820 LET dy=R*SIN (PI/180*a)*(COS (PI/180*(b+db))-COS (PI/180*b))
830 LET dz=R*COS (PI/180*a)*(COS (PI/180*(b+db))-COS (PI/180*b))
840 IF x>z/5.6 THEN LET x=z/5.6
850 IF (x=dx)>z/5.6 THEN LET dx=z/5.6-x
860 IF y>z/8.3 THEN LET y=z/8.3
870 IF (y+dy)>z/8.3 THEN LET dy=z/8.3-y
880 IF x<-z/5.6 THEN LET x=-z/5.6
890 IF (x+dx)<-z/5.6 THEN LET dx=-z/5.6-x
900 IF y<-z/9 THEN LET y=-z/9
910 IF (y+dy)<-z/9 THEN LET dy=-z/9-y
920 LET xp=x*d/z: LET yp=y*d/z
930 PLOT xp*p+128,yp*p+87
940 LET dk=d/(z+dz)-d/z
950 LET dxp=dx*d/z+x*dk: LET dyp=dy*d/z+y*dk
960 LET e=ABS ((z-d)/200)
970 DRAW INK e;dxp*p,dyp*p
980 NEXT b
990 NEXT a
1000 GO TO 70

small title
b0=90° - places the first figure in the plane x=x0 - that is, 'edge-on' to the screen.
This enables us to draw figures from the bundle of vertical planes - the plane intersection is placed at co0ordinates x0,z0.
  The program could be modified easily to draw a bundle of planes with horizontal intersection by swapping around the longitude and latitude. We include some further examples of parameters asked for in the INPUT statements (by the program given in last 		month's article) which can be effective when combined with translation and rotation.
  Remember that all dimensions are in millimetres and will be drawn accurately in perspective for the parts of the 3D 'object' which lie within the viewing pyramid. This means that the value of R must be less than or equal to 62 for the parts of the object which lie at z0=500 - that is, the screen depth.
  Note that selection of z0=500 will make the front sections of the objects lie in front of the screen and therefore, the top and bottom parts of the object will be subject to 'clipping'.
  Translation (for example, along the z-axis) can be effectively demonstrated by the addition of a z0 loop in the program:

 90 REM 'Zoom' example 		...
185 LET z0=500
...
440 LET Z0=z0+100: IF z0>1100 THEN GO TO 90
443 GO TO 190

The same can be done for translation along the x and y axes.
  Combined translation (in the x-axis) and rotation around the vertical axis (longitude) can be done in the following way:

110 REM 'Combined translation mix and longitude rotation'
...
185 LET x0=-45
188 LET b0=b0+10: REM 'Next object will be rotated 0'
440 LET x0=x0+22.5: IF x0>45 THEN GO TO 90
443 GO TO 188
 BENCH ROUND TABLE
 TOPLEGSSHELVESCARPET/ SHADOWTOPBOTTOM
z0
R
x0
y0
sa
sb
b0
a0		 700
200
-90
-45
1
2
90
0		 700
200
-70
-45
1
2
90
0		 500
10
-80
-45
1
2
0
0		 900
10
-80
-45
1
2
0
0		 500
8
-80
-53
1
4
90
45		 900
8
-80
-53
1
4
90
45		 600
37
90
-40
1
4
90
45		 600
31
80
-40
1
4
90
45		 600
8
85
-40
1
4
90
0		 600
8
85
-20
1
4
90
0		 600
8
85
-50
1
4
90
0		 600
40
0
-62
1
11
0
0		 600
30
0
-45
1
15
0
0		 600
12
0
-53.5
1
4
45
45
 VERTICAL (V)HORIZONTAL (H)(V)
Some examples of the kind of shapes you can produce with the program given with this article. You could also try producing some of your own shapes with a twist of translation loops (R=R(y)) - have a go, they're highly recommended.

Home Contents KwikPik