
Using the curve tool in the Microsoft Paint program.
William Overington
Copyright 2002 William Overington
Wednesday 12 June 2002
The curve tool in the Microsoft Paint program can be used to produce a variety of curves.
An interesting aspect of the curve tool is that it appears to be implemented using an underlying mathematical method which uses Bézier curves.
Once one knows this and understands a method of using the curve tool which I have devised for this series of workshops on using the Paint program, then the range of pictures which one can produce using the curve tool is very much increased.
Although the software is just the same, this method of using the curve tool adds a precise drawing capability using the curve tool such that the range of additional possibilities is almost as if a special plug-in had been added to the Paint program!
For readers who choose to use this method of using the curve tool in conjunction with one or more of the outlines which are available from the web page entitled
A collection of outlines of shapes for use with the Microsoft Paint program.
which is available in this webspace, there are considerable artistic possibilities which are now possible using the Paint program.
Bézier curves are mathematical curves about which there is a lot of information on the web. A search at http://www.yahoo.com using the word Bezier as the search word (that is, without the acute accent on the e) provides various links for those readers interested in studying the underlying mathematics, yet there is no need to study the mathematics in order to use the technique which is described in this present document.
Apart from saying that Bézier curves were invented in relation to designing the surfaces of cars and that they are now used in other applications, such as the way that a TrueType fount stores the designs of the character glyphs within a .ttf file, I shall not here go further into the general theory of Bézier curves. Readers who are interested in the underlying mathematics may find that information elsewhere. Here I explain in basic terms only that which one needs to know of the theory of Bézier curves to use the curve tool of the Paint program effectively. Nevertheless, the mathematics of Bézier curves is fascinating and is well worth studying.
For the purposes of this workshop one may conveniently think of a Bézier curve as either a three point Bézier curve or as a four point Bézier curve.
Using my own definitions for the purposes of a general introduction to applying Bézier curves in this workshop, here are convenient ways to think of Bézier curves.
A three point Bézier curve may be thought of as a curve starting at a point A and finishing at a point B, its route from A to B being influenced by a point P, though not actually passing through the point P.
The curve starts off from A, the first tiny piece heading for the point P.
The curve finishes at B, the last tiny piece as if it had come from point P.
A four point Bézier curve may be thought of as a curve starting at a point A and finishing at a point B, its route from A to B being influenced by point P and by point Q, though not actually passing through the point P or through the point Q.
The curve starts off from A, the first tiny piece heading for the point P.
The curve finishes at B, the last tiny piece as if it had come from point Q.
Given those workshop definitions, how may one use the curve tool of Microsoft Paint to draw a Bézier curve? Here are some examples which illustrate the method and also provide an insight into the route that the curve takes when leaving point A and arriving at point B.
Please use 8x magnification in order to try these examples in order to achieve accuracy, viewing them at 1x magnification when they are completed. If you can work satisfactorily at a smaller magnification later, then you could draw larger curves.
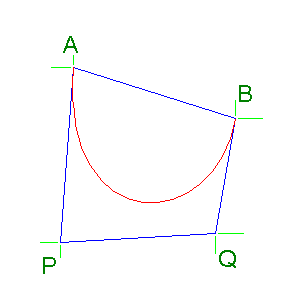
For a three point Bézier curve, first draw a construction triangle. Now, select the curve tool from the tool box of Paint.
Move the mouse pointer over point A.

Press the mouse button.
Move the mouse pointer over point B.
Release the mouse button.
Move the mouse pointer over point P.
Press the mouse button.
Release the mouse button.
Press the mouse button again.
Release the mouse button.
Please note how the curve leaves point A initially heading for point P, then gradually turns so that it arrives at point B from the direction of point P.
For a four point Bézier curve, first draw a construction quadrilateral. Now, select the curve tool from the tool box of Paint.
Move the mouse pointer over point A.

Press the mouse button.
Move the mouse pointer over point B.
Release the mouse button.
Move the mouse pointer over point P.
Press the mouse button.
Release the mouse button.
Move the mouse button over point Q.
Press the mouse button.
Release the mouse button.
Please note how the curve leaves point A initially heading for point P, then gradually turns so that it arrives at point B from the direction of point Q.
Here is another four point Bézier curve produced using the same points, yet with the order of using point P and point Q interchanged.
Move the mouse pointer over point A,
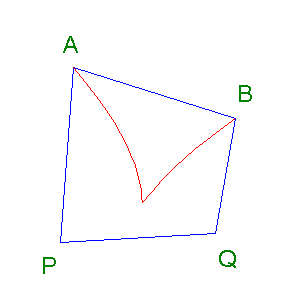
Press the mouse button.
Move the mouse pointer over point B.
Release the mouse button.
Move the mouse pointer over point Q.
Press the mouse button.
Release the mouse button.
Move the mouse button over point P.
Press the mouse button.
Release the mouse button.
Here is a picture showing the two previous four point Bézier curves together in one picture.
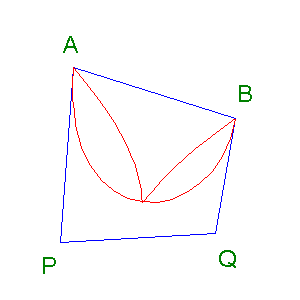
In some circumstances a four point Bézier curve can produce a loop effect.

Here is an illustration showing how such a loop relates to the other Bézier curve of the pair.

Another interesting situation is where the points P and Q are on opposite sides of the line AB.
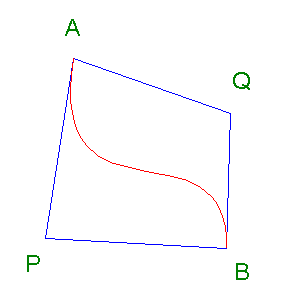
In the illustrations I have added the letters to indicate the points. There is no need to add letters when using the method. Indeed, there is no need to draw the lines of a triangle or a quadrilateral, one just needs the points upon which to click.
However, drawing construction lines can be very useful particularly where one uses a shape such as a square or a star in order to produce a supply of points to use in drawing a number of Bézier curves all in one picture.
Construction lines can be removed from the picture at a later stage if so desired. Indeed, the use of symmetrical mathematical shapes to provide construction points for a number of Bézier curves which are all drawn on the same picture in a precise manner is the feature of using the curve tool in the manner explained in this workshop which offers great possibilities for producing ornate designs and original art using the Paint program.
 In constructing the diagrams displayed within this document I used a technique of adding
guidelines, then using them so as to assist in choosing the correct place to press
and release the mouse button.
Once the correct curves were drawn, the guidelines were deleted.
Here is a sample file showing how the guidelines are located.
The green colour is so that the guidelines both show up and also contrast well with the
crosswires of the mouse pointer.
I found the guidelines helpful.
The diagrams above were produced using 2x magnification.
Nevertheless I did find it necessary to sometimes view what I had produced at 8x magnification
and then use Edit Undo and try again until I got a picture with which I was pleased.
In constructing the diagrams displayed within this document I used a technique of adding
guidelines, then using them so as to assist in choosing the correct place to press
and release the mouse button.
Once the correct curves were drawn, the guidelines were deleted.
Here is a sample file showing how the guidelines are located.
The green colour is so that the guidelines both show up and also contrast well with the
crosswires of the mouse pointer.
I found the guidelines helpful.
The diagrams above were produced using 2x magnification.
Nevertheless I did find it necessary to sometimes view what I had produced at 8x magnification
and then use Edit Undo and try again until I got a picture with which I was pleased.
The Paint program has been designed with great mathematical precision within it, the method described in this workshop enables an end user to use the Paint program in a manner which is not usually envisaged for the Paint program.
Here are some examples of using the curve tool with some four point Bézier curves, which curves were all produced using just the four corner points of a square as the construction points. The square is 80 pixels along each edge. The pictures are 200 pixels by 200 pixels. These pictures are intended as items of art, I have filled various areas with colour. They are included as some examples of the type of designs which can be produced using this technique. All three were produced using 6x magnification with, having chosen red, the colour box not displayed. This meant that the display of the square almost filled the work area, using a screen display with a total display area of 800 pixels wide by 600 pixels high.



As a tailpiece to this document is a design produced using a seven-pointed star and some four point Bézier curves. The seven-pointed star is from the collection of outlines of shapes elsewhere in this webspace. It is a seven-pointed star with star selector equals 3, and is, in fact, the third along from the left in the top row of the graphic of those stars. Each of the Bézier curves is produced by using two of the star points as construction points. Once the Bézier curves have been completed, the original star is deleted, and the loops are filled with a different colour. I did find it necessary to add one red pixel in by hand. This was in about the 11 O'clock position, where there was a gap. The picture was produced using a 300 pixel by 300 pixel square picture. This was trimmed to 200 pixels by 200 pixels once the final design had been produced.
This is but one example of what is possible.
The use of the method of using the curve tool described in this document using an outline of a shape obtained from those available elsewhere in this webspace can produce many original artistic designs.
An interesting aspect of this is that the various polygons and stars are all regular mathematical shapes. A Bézier curve is constructed according to precise mathematical reasoning. So, in a way, any graphic produced by drawing Bézier curves using construction points on regular mathematical shapes is a matter of discovering what already exists awaiting discovery.
However, there are many possible permutations of choices of construction curves so it may be that if you produce such a design then it might be that you are the first person ever to produce that design.
Deciding to colour in some parts of the design then produces a work of art that may be unique.
Other designs can be produced using construction points that are not located on a regular mathematical shape.

It is hoped that this workshop will be helpful in enabling readers to gain enjoyment from using the Paint program and will hopefully lead to them producing some interesting designs.
Copyright 2002 William Overington
This file is accessible as follows.