The Maths-Classics project

Assignment 8

The golden number

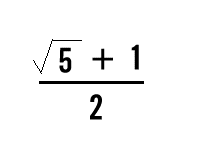(For more advanced mathematicians!)

The Greeks believed that a special ratio of numbers when used in the design of buildings, paintings, sculpture etc. would automatically make them beautiful. This is the GOLDEN NUMBER:

 

• Work out this number as a decimal. What do you notice about it?
  The relationship of this number to 1 is called the GOLDEN RATIO or the GOLDEN SECTION. Mathematicians refer to this number by the Greek letter t (tau): what other number with a similar property is known by a Greek letter?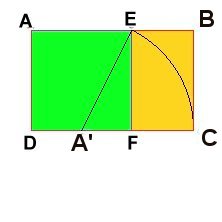

• Draw your own GOLDEN RECTANGLE following these instructions: you'll need a pencil, ruler, compass, and a right-angle triangle.

  
  First draw a square, AEFD, any size you like. Then divide the line DF in half at A'. Then, with the compass and using A' as center, draw an arc from E down to C, which intersects the extension of line DF. With your triangle, draw BC perpendicular to AB, meeting the extension of line AE at B. The new ABCD rectangle is a golden rectangle, in which AB is divided by E in exactly the golden section:

  AE:AB = EB:AE

  That is, the ratio of the longer part to the whole is equal to the ratio of the shorter part to the longer part.
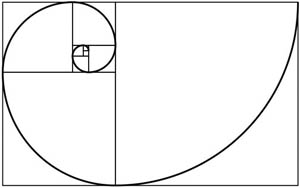  Check its measurements: AB divided by AE should give you something close to the same result as you got above (depending on the accuracy of your measuring!) The rectangle EBCF is of course also a golden rectangle, and can be divided up in the same way - and so on ad infinitum. Your teacher may be able to show you how these nested rectangles can be used to construct a spiral - exactly the same spiral as Nature has used in the design of a snail shell!

  

• Another way to get at the Golden ratio is using a FIBONACCI SEQUENCE:
  1, 1, 2, 3, 5, 8, ...
  Write out the first twenty-five terms of the sequence.
  Take the terms two at a time and divide the larger by the smaller (ie 2 by 1; 3 by 2, 5 by 3 etc) working as accurately as you can. Record the answers that you get.
  What do you notice about these values?

• Measure the sizes of various rectangular object e.g. books, windows,doors, photographs, etc. Is the ratio of the sides near the value of the Golden Ratio? Record your results. A piece of A4 paper is a good place to start (You can measure it AND record your results on it!)!

• Take a stem of a plant ( ask the owner before you remove it !!).
  Measure the distance between successive leaves, record the distances.
  Are the ratios of pairs of distances interesting?

• Talk to your Art teacher about the Golden Ratio and its significance in Art. Look at where the subject of a picture is and see how the Golden Ratio is used by artists. Include some pictures from newspapers or photocopies of well-known paintings. Click here for a picture of the end facade of the Parthenon analysed for golden rectangles - the entire design of the Parthenon is based on it, of course.[http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/parthenonPhi.gif]

  Here is Norham Castle by J M W Turner: what do you notice?

  

• Visit these websites for further information:

  http://www.textism.com/bucket/fib.html (Brilliant animation! May be slow loading - but well worth the wait)
  http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fibInArt.html